Nearest
Neighbor Analysis
In past newsletter articles,
I've borrowed concepts from statistics, such as serial dependency and
significance testing, and demonstrated their application to trading. This
month I'm going to introduce another idea from statistics. The nearest neighbor
concept can be found in nonlinear modeling, chaos research, and statistical
pattern recognition. While these topics can be complex, the basic idea of
nearest neighbor analysis is not difficult to understand.
In one respect, the nearest
neighbor concept is a data analysis technique. It's a way to focus an analysis
on the data that are closest in some sense to the conditions of interest. In
statistical pattern recognition, for example, the objective is to design a
"classifier," which discriminates between the patterns you're trying to identify
and all other patterns encountered by the classifier. The classifier is obtained
by fitting a probability density function to a set of data samples. The "k
nearest neighbor" technique estimates the probability density function for
the classifier point by point using the k data samples nearest to each
point [see reference 1]. The alternative would be to use a
mathematical equation to represent the classifier. If an equation were
available, the classifier would be fit simultaneously to all available data
samples, rather than just the k samples nearest the evaluation point. So called
"nonparametric" methods, like k nearest neighbor, are typically used when a
parametric method -- an equation -- is not available. In trading the markets,
viable parametric methods are rare.
In a simple sense, the nearest
neighbor approach is analogous to an N-period moving average. The moving average
is calculated on each bar using the N bars nearest to the current bar.
Similarly, the k nearest neighbor estimate is calculated from the k "neighbors"
nearest to the point of interest. Nearest neighbor estimates are local
estimates, like a simple moving average, centered around the point of interest
and recalculated using different neighbors at every other point of
interest. One advantage of this localization approach for trading is that
it tends to adapt the results to current market conditions.
There are several ways in which
nearest neighbor analysis can be applied to trading, including the
following:
-
Use the nearest neighbor
estimate as a price prediction, and incorporate the prediction into a trading
system.
-
Use the nearest neighbor
price prediction as an indicator or guide to trading.
-
Use a nearest neighbor
search to increase the computational efficiency of data intensive market
modeling methods, such as neural networks or kernel regression; see reference
2.
-
Optimize a trading
system's parameters over the N nearest neighbors to adapt the parameter values
to current market conditions.
-
Optimize
a system's position sizing parameters over the N nearest neighbors to
adapt the position sizing to current market conditions.
I'll develop idea #1 below, but
before I do that, I want to briefly discuss the last two ideas. The usual
approach to tailor system parameter values to current market conditions is
to use "walk-forward" optimization. The idea of walk-forward optimization is
that you optimize the parameter values on a past segment of market
data, then test the system forward in time on data following the
optimization segment. You evaluate the system based on how well it performs on
the test data, not the data it was optimized on. The process can be repeated by
moving the optimization and test segments forward in time. The premise of
walk-forward optimization is that the recent past is a better foundation for
selecting system parameter values than the distant past. The hope is that the
parameter values chosen on the optimization segment will be well suited to the
market conditions that immediately follow. The problem with this approach is
that when market conditions change -- say, from bull market to bear market --
you may find yourself optimizing on one set of market conditions while trading a
completely different set of conditions. In this case, there's no good reason to
expect that the walk-forward results will be similar to the optimized
results.
Nearest neighbor analysis
provides an alternative to this approach. Instead of optimizing over all data in
the recent past, you can select a sampling of trades over a longer period of
time based on how close the trades are in the nearest neighbor sense to the
current market conditions. For example, choose a set of indicators, such as
momentum, ADX, moving averages, etc. Evaluate the indicators on the current bar.
Then evaluate the indicators on the bar preceding each past trade. Select the N
(say, 30 or so) trades with indicator values closest to those on the current
bar. Optimize the system parameter values over these 30 trades. As
the parameter values are varied during the optimization, different
trades may be produced, so the 30 trades chosen to evaluate the system may
change from optimization iteration to iteration.
Once the optimal parameter
values are found, the profit/loss from the next trade can be recorded. As in
walk forward optimization, this trade will be out-of-sample, meaning it is
generated without the benefit of hindsight. After each trade is complete, the
process can be repeated for each new trade. This means that new parameter
values will be generated for each trade. If the purpose is to evaluate
a trading system, you would use the out-of-sample trade results to evaluate the
system, rather than the optimized results on the N
nearest neighbors. While this procedure is more complex than
traditional walk forward optimization, the nearest neighbor approach may
provide a more reliable way to determine system parameter values that adapt to
current market conditions.
The same idea can be applied to
position sizing. Let's say you're using a fixed fractional position sizing
technique, in which a percentage of the account equity is risked on each trade.
Typically, one would use all available trade profit/loss data to compute the
best fixed fraction for future trading. However, instead of using all trades,
why not use the N nearest neighbors; i.e., the N trades that are closest to
current market conditions as determined by a set of indicator values? The
procedure is the same as described above, except that you're optimizing on the
fixed fraction (or whatever position sizing parameter you want) rather than on
the system parameter values. In this way, you adapt the fixed fraction to
current market conditions.
A Nearest Neighbor
Trading System
I may have more to say on these
techniques in a later newsletter, but for now, I want to demonstrate how nearest
neighbor prediction can be used to develop a trading system. The basic idea is
to define a
pattern using trading indicators and find the N patterns that are closest to the
pattern on the current bar. You then decide to buy or sell based on whether the
average market move following the N patterns is up or down [reference 3]. For
example, consider the following momentum indicators:
I1 = (C -
C[1])/I1Max
I2 =
(C - C[2])/I2Max
I3 = (C -
C[3])/I3Max
I4 = (C -
C[5])/I4Max
where C is the closing price on
the current bar, C[i] is the close i bars ago, and I1Max - I4Max are the
maximum values of I1 - I4. The momentum values are normalized by the maximum
values so that each indicator will be in the range [-1, +1]. The first step is
to evaluate I1 - I4 on the current bar. The indicators are then evaluated on
each prior bar, and the following error values are calculated:
Ei = (I1 -
I1[i])^2 + (I2 - I2[i])^2 + (I3 - I3[i])^2 + (I4 - I4[i])^2
where Ei is the error on the
bar i bars ago, and I1[i] - I4[i] are the indicator values i bars ago. The
N nearest neighbors are the i's (that is, the bars) that provide the
smallest error values, Ei.
As a result, we end up with a
set of N bars with indicator patterns similar to the pattern we have on the
current bar. The final step is to see which way the market moved following each
of the N patterns. If, for example, the average move following the N patterns is
10 points up in two days, then we might want to buy the market and hold for two
days in expectation of a similar move.
I wrote a simple system based
on this idea and tested it on the E-mini S&P 500 futures. The EasyLanguage
code for the system is shown below.
{
N-N Predict ("Nearest Neighbor
Prediction")
This system searches for the N nearest neighbors to a
pattern consisting
of a set of indicator values. The average market
move following the N patterns
is taken as the
prediction.
If the average prediction is up, the system buys and exits two days later.
If
the average prediction is down, the system sells and covers two
days later.
The system also writes out the prediction on each bar for the next several
days.
Copyright 2004 Breakout Futures
www.BreakoutFutures.com
mrb@BreakoutFutures.com
}
Input: NNN
(50), { Number of nearest neighbors used in
prediction }
NPredict
(5), { Number of days forward to predict
}
FName
("C:\NNResults1.csv"); { file name to write results to
}
Array: Errors[500, 2](0), { Error of patterns
relative to current bar }
NNBars [50](0), { Bar numbers of nearest neighbors
}
CPredict [20](0); {
Prediction of close 1 to 20 days in future }
Var: Ind1
(0), { Value of indicator 1
}
Ind2
(0), { Value of indicator 2
}
Ind3
(0), { Value of indicator 3
}
Ind4
(0), { Value of indicator 4
}
I1Max
(0.01), { Max value of indicator 1
}
I2Max
(0.01), { Max value of indicator 2
}
I3Max
(0.01), { Max value of indicator 3
}
I4Max
(0.01), { Max value of indicator 4
}
SumC
(0), { Sum of predicted closes
}
MinErr
(0), { Minimum error
}
MAXBARS
(500), { Max dimension of Error array
}
MAXNNN
(50), { Max dimension of NNBars array
}
MAXPRED
(20), { Max dimension of CPredict array
}
NBars
(0), { Number of bars to look back
}
NoMatch
(True), { Logical flag for searching
}
ii (0),
{ loop counter }
jj (0),
{ loop counter }
kk (0),
{ loop counter }
StrOut (""); { output character string
}
{ Initialize file on first bar }
If BarNumber
= 1 then Begin
FileDelete(FName);
StrOut = "Date, Close, PredDay1, PredDay2, PredDay3, PredDay4, PredDay5" +
NewLine;
FileAppend(FName,
StrOut);
End;
NBars = MinList(MaxBarsBack - 20,
MAXBARS);
{ Define indicators }
Ind1 = C -
C[1];
Ind2 = C - C[2];
Ind3 = C - C[3];
Ind4 = C -
C[5];
{ Loop over prior bars to find max indicator values
}
for ii = 1 to NBars Begin
if Ind1[ii] >
I1Max then
I1Max =
Ind1[ii];
if Ind2[ii] > I2Max
then
I2Max =
Ind2[ii];
if Ind3[ii] > I3Max
then
I3Max =
Ind3[ii];
if Ind4[ii] > I4Max
then
I4Max =
Ind4[ii];
End;
{ Calculate errors }
for ii = 1 to NBars
Begin
Errors[ii - 1, 0] = Square((Ind1 - Ind1[ii])/I1Max)
+ Square((Ind2 - Ind2[ii])/I2Max)
+
Square((Ind3 - Ind3[ii])/I3Max) + Square((Ind4 -
Ind4[ii])/I4Max);
Errors[ii - 1, 1] = ii -
1;
End;
{ Take the smallest NNN values as the nearest neighbors
}
for ii = 0 to MinList(NNN - 1, MAXNNN - 1)
Begin
MinErr = 100 * Errors[0,
0];
for jj = 0 to NBars - 1
Begin
if Errors[jj, 0] <
MinErr then
Begin
NoMatch =
true;
for
kk = 0 to ii
Begin
if Errors[jj, 1] = NNBars[kk]
then
NoMatch =
false;
End;
if
NoMatch then
Begin
MinErr = Errors[jj,
0];
NNBars[ii]= Errors[jj,
1];
End;
End;
End;
End;
{ Calculate prediction for next NPredict bars
}
for ii = 0 to MinList(NPredict - 1, MAXPRED - 1)
Begin
SumC = 0;
for jj =
0 to MinList(NNN - 1, MAXNNN - 1)
Begin
if (NNBars[jj] - ii -
1) > 0
then
SumC
= SumC + (C[NNBars[jj] - ii - 1] - C[NNBars[jj]]);
End;
CPredict[ii] = C +
(SumC/NNN);
End;
{ Write out predictions }
StrOut =
NumtoStr(Date, 0) + "," + NumToStr(C, 2) + "," +
NumtoStr(CPredict[0], 2) + "," + NumToStr(CPredict[1], 2) + ","
+
NumtoStr(CPredict[2], 2) + "," + NumToStr(CPredict[3], 2) + ","
+
NumToStr(CPredict[4], 2) + NewLine;
FileAppend(FName,
StrOut);
{ Buy if predictions are up; sell if down
}
if CPredict[0] > C and CPredict[1] > C and CPredict[2] > C
then
Buy next bar at C limit;
if CPredict[0] < C and CPredict[1] < C and
CPredict[2] < C then
Sell short next bar at C
limit;
if BarsSinceEntry = 2 then Begin
Sell this bar on close;
Buy to cover this bar on
close;
End;
Fig. 1. EasyLanguage
code for nearest neighbor system, "N-N Predict".
The N-N Predict system uses the
indicators I1 - I4 given above. It calculates these indicators on each bar and
stores the errors, Ei, in the Errors array. The first column of this
two-dimensional array holds the error value on each bar; the second column
stores the bar number. The error array is then searched for the NNN nearest
neighbors (bars) with the smallest errors. The predicted closing price in the
future for the next NPredict bars is calculated by averaging the price
changes following the nearest neighbors and adding the average price change
to the current close. For example, if the average price change two days after
the nearest neighbors is +4 points, and the current close is 1143.00, then the
predicted close two days from the current close would be 1147.00. A prediction
is made for each bar following the current close up to NPredict bars, although
the predictions for only the first five bars are written out to the text
file.
After the predictions are made,
the trades are placed. A long trade is placed if the predicted close for each of
the next three bars is higher than the current close. A short trade is place if
the predicted close for each of the next three bars is lower than the current
close. The entry orders are placed at the prior close using a limit order to
ensure that the entry price is no worse than the prior close. The trade is
exited two days later on the close. No protective stop order is
used.
In order to make sure the
system has enough data to identify a good set of nearest neighbors, it's
necessary to set the look back length (MaxBarsBack in TradeStation) to a
large number. I found that a look back length of about 150 generated good
results using 50 nearest neighbors. With a larger look back length, the system
will be basing the predictions more on the past, whereas a shorter length means
the samples will be taken from more recent bars.
Without including any costs for
slippage or commissions, the following results were obtained over 1000 bars on
daily data (symbol @ES in TradeStation 7.2), ending on 2/25/04:
Net Profit:
$39,968
Profit Factor:
1.37
No. Trades:
277
% Profitable:
57%
Ave. Trade:
$144
Max DD:
-$13,700
The equity curve is show
below.
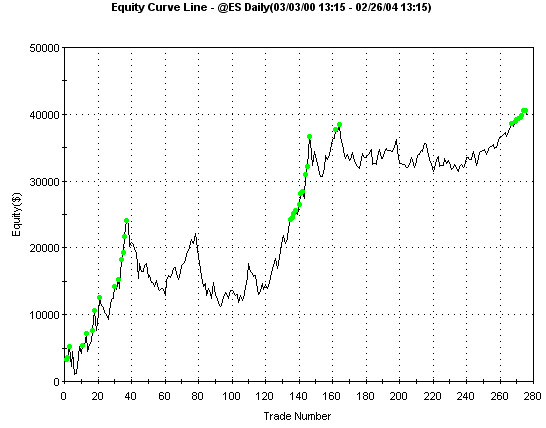
Fig. 2. Equity
curve for "N-N Predict" system on the E-mini
S&P.
The N-N Predict
system is a simple system designed to illustrate the concept of using nearest
neighbor prediction as the basis for a trading system. Nonetheless, it works
reasonably well over data including both bull and bear markets. Also, once
a set of indicator values is chosen, there are few parameters that require
adjustment. A small number of parameters tends to imply that a system is
less likely to be curve fit to the market. The only explicit parameter is the
number of nearest neighbors used to compute the price predictions. I found
that 50 worked better than 40, which was better than 20 or 30. I didn't try more
than 50 nearest neighbors, but as this number approaches the length of the look
back period, the prediction will be based on a greater and greater fraction of
the look back period until the prediction is nothing more than an average
of all price changes in the look back period.
In addition to
the number of nearest neighbors, the performance of this system will depend on
the look back length. It may be that the ratio between the look back length and
the number of nearest neighbors is important. With the values I chose here, the
ratio is 3:1. Of course, the selection of indicators for the nearest neighbor
patterns is very important. I chose simple momentum indicators for N-N Predict.
Any indicator could be used, including moving averages, stochastics, ADX,
Bollinger bands, etc. In fact, the "neural network" indicator I developed in the
last newsletter would be an interesting indicator to include in this type of
system.
References:
-
Keinosuke
Fukunaga, Introduction to Statistical Pattern Recognition, 2nd Ed., Academic
Press Inc., San Diego, CA, 1990.
-
John R. Wolberg, Expert
Trading Systems, John Wiley & Sons, Inc., New York, 2000.
-
Hans Uhlig, Nearest Neighbor
Prediction, Technical Analysis of Stocks & Commodities, November 2001, pp.
56-61.
Correction
In December, I
forgot to include the EasyLanguage code for the tanh function, which was used in
the neural network system. Here it is:
{
tanh function.
Return an approximation to
the hyperbolic tangent function. The
approximation is given on p. 219
of CRC Standard Mathematical
Tables, 26th edition.
Mike Bryant
Breakout
Futures
www.BreakoutFutures.com
Copyright 2003
}
Input:
x (NumericSimple), { input to function
}
NTerms
(NumericSimple); { # terms in series }
Var: pi
(3.1415926536),
Sum
(0),
ii (0);
Sum = 0.;
For ii = 0 to NTerms
Begin
Sum = Sum + 1./(Power(((ii + 0.5)*pi), 2) + Power(x,
2));
End;
tanh = Sum * 2 * x;