Nonlinear Volatility Exits
Trading
system exits based on volatility are fairly common. In fact, I discussed
both money management stops and profit targets based on the average true
range (ATR), a common measure of volatility, in the December 2007 issue
of The Breakout Bulletin. More recently, I wrote an article for the July
issue of Active Trader magazine in which I discussed using
volatility-based stops in conjunction with fixed fractional position
sizing (http://www.activetradermag.com/index.php/c/Trading_Strategies/d/Adapting_position_size_to_volatility).
Linear Volatility Exits
Often, the size of a
money management stop or profit target is calculated as a multiple of
the average true range (ATR); e.g., 2 x ATR. This provides the stop or target size in points.
For a money management stop, you would determine the stop price by subtracting the result from the entry price for a long trade or adding
it to the entry price for a short trade. Similarly, when calculating a
profit target in terms of volatility, you would determine the target
price by adding the multiple of ATR to the entry price for a long trade
or subtracting it from the entry price for a short trade.
By calculating the exit in this
manner, the size of the exit is normalized by market volatility. That
means it automatically adapts to the market's volatility. When the
market volatility changes, so does the stop size, without requiring any
adjustment from the trader. Another advantage of volatility-based stops
is that they make it easier to apply the same parameter values across
different markets. For example, if you optimize a trading system across
corn, crude oil, and T-bonds, the best stop size for each market may be
very different in dollar terms. If you normalize by volatility, however,
you may be more successful in applying the same volatility multiplier to
calculate the stop size across all three markets. A stop specified as
twice the ATR, for example, would generate a much larger stop in crude
oil than in corn because crude oil has a much larger ATR in dollar
terms.
This type of volatility exit is linear in
that the size of the exit is a linear function of volatility, as
represented by the ATR. With a linear exit, as the volatility increases,
the size of the exit (stop size or target size in points) increases in
direct proportion to the volatility. Likewise, when the volatility
drops, the stop or target size decreases in direct proportion to the
volatility. While this is the most common way to calculate these types
of exits, it's not necessary to limit our exit calculations to linear
functions of volatility.
Nonlinear Functions of
Volatility
The simplest form of a
nonlinear volatility exit can be represented by the following equation:
Exit Size (points) = a0 + a1 *
ATR + a2 * ATR2
where a0, a1, and a2 are
constants. The last term, a function of the ATR squared, provides the
nonlinearity. The first term, a0, is a kind of offset. It scales the
exit size up or down by a fixed amount. If the other constants, a1 and
a2, are zero, the exit size would be fixed at a0; e.g., a fixed stop
size of 5 points. With a0 and a2 both equal to zero, this equation
reduces to the linear volatility exit discussed above. This equation
encompasses fixed size exits, linear exits, and nonlinear exits.
Fig. 1 illustrates the
differences between the linear and nonlinear volatility exits as the
volatility changes. The red line depicts the standard linear volatility
exit with a positive offset (a0 > 0). As volatility increases, the exit
size increases in direct proportion. The green and violet lines
illustrate the nonlinear exit. The green line demonstrates how the exit
size increases faster than with the linear exit when a2 is a positive
number (a2 > 0). When a2 is a negative number (a2 < 0), the exit size
still increases with volatility but at a much slower rate. For this
exit, the exit size would eventually begin to decrease with increasing
volatility.
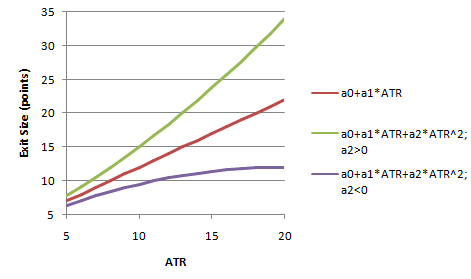
Fig. 1.
Exit size in points for linear and nonlinear exits. The nonlinear exit
will change faster or slower than the linear exit depending on the value
of the coefficient a2.
The only problem with this exit
size equation is that it's not completely normalized by volatility the
way the linear volatility exit is. For example, the first term, a0, is
given in points, rather than as a function of ATR. Also, because ATR
values can vary widely by market, the coefficient for the third term,
a2, will likewise vary widely for different markets. This would make it
difficult to apply this equation across different markets with the same
parameter values.
A normalized version of the
nonlinear exit size equation can be developed if we first normalize the
ATR itself. To do this, we can divide the ATR by a longer-term ATR. For
example, perhaps the original ATR is averaged over 10 bars, whereas a
longer-term ATR is averaged over 200 bars. The latter represents the
long-term average of the market's true range, which should vary much
more slowly from bar to bar than the original ATR.
A volatility-normalized version
of the exit size equation can be written as follows:
Exit Size Norm (points) =
ATRlt * [a0 + a1 * (ATRst/ATRlt) + a2 *
(ATRst/ATRlt)2]
where a0, a1, and a2 are
constants, ATRst is the short-term ATR, and ATRlt
is the long-term ATR.
The normalized equation will
behave very similarly with respect to volatility as the original
nonlinear exit equation, depicted in Fig. 1. Moreover, the three
constants -- a0, a1, and a2 -- are independent of volatility, which
makes it more likely that the same values could be used successfully
across different markets.
The Rationale for Nonlinear
Exits
You might be wondering why a
nonlinear exit would be better than an exit based simply on a multiple
of the ATR. First, the rationale for any volatility exit is that the
volatility, based on the ATR in our case, represents the random
fluctuations, or noise, in the market. Generally speaking, you don't
want your exit to be influenced by random fluctuations. Making the stop
or target size a function of volatility helps prevent the exit from
being triggered by this noise while at the same time automatically
adapting to changes in the size of the random movements.
It's the changes in volatility
that provide a rationale for the nonlinear exits. If the volatility
never changed, there would be no difference between the linear and
nonlinear exits. In this case, the second and third terms in the
normalized equation would be constants, so this equation would be
equivalent to a linear function of ATR. However, if the volatility is increasing or
decreasing, the nonlinear equation is capable of anticipating future
changes in volatility. In particular, if for the market being traded,
the volatility tends to trend, so that once it starts to increase, it
tends to continue increasing, then we would want a nonlinear exit
similar to the green line in Fig. 1. In this case, high volatility
results in a larger exit size than the linear exit would provide. In
effect, the nonlinear exit is expecting that the volatility will
increase further, so it provides a larger exit than the linear exit.
Similarly, if the market
volatility tends to be mean-reverting -- high volatility implies the
volatility will fall, and vice-versa -- then we would want a nonlinear
exit similar to the red line in Fig. 1. In this case, for high
volatility, the nonlinear exit will provide a smaller stop than the
linear exit. In effect, the exit is anticipating a decline in
volatility.
In practice, we don't need to
know ahead of time whether the volatility tends to be trending or
mean-reverting because the constants in the exit size equation will have
to be determined via some sort of optimization. If we find that the best
value of a2 is greater than zero, we know that the volatility tends to
trend. Likewise, if our optimal value of a2 is less than zero, we know
that the volatility tends to be mean-reverting. Whether the volatility
is trending or mean-reverting may very well depend on the market, the
time period studied, and the averaging period for the ATR.
Stop and Target Prices
The exit size equation provides
the size of the exit in market points. The exit size is then used to
determine either stop prices or profit target prices. To determine the
stop prices, the following equations can be used:
Stop Price (long trade) = Entry
Price - Exit Size Norm,
Stop Price (short trade) =
Entry Price + Exit Size Norm.
The price for a profit target
can be calculated as follows:
Profit Target Price (long
trade) = Entry Price + Exit Size Norm,
Profit Target Price (short
trade) = Entry Price - Exit Size Norm.
A TradeStation Example
To test the nonlinear
exits and compare
them to linear exits, I wrote a simple system in TradeStation's
EasyLanguage. The system, called NonlinearExits, is available on my
downloads page. NonlinearExits is a
trend-following system that enters long on the next bar if the close is
above the moving average and above the highest high of the last NChan
bars plus some fraction of the ATR. Once long, the trade is exited after
NBExit bars or at the nonlinear stop or target. The reverse logic is
used for short trades. The normalized version of the nonlinear exit was
used.
I tested the stops and
targets separately by commenting out the exit not being tested. The exit
at N bars from entry was used throughout. The nonlinear and linear exits
were compared on three markets: crude oil (symbol @CL.P), Yen (symbol @JY.P),
and T-bonds (symbol @US.P). All data consisted of daily bars,
backadjusted in TradeStation 8.2. For crude oil and Yen, 20 years of
data were used; 15 years were used for T-bonds. $75 round-turn trading
costs were deducted per contract. The short and long-term ATR lengths
were set to 10 and 200 bars, respectively.
To establish a baseline, I
first optimized the system on each market separately with the volatility
exits (stop and target) commented out so that only the N-bars-from-entry
exit was active. I then optimized the linear stop first, followed by the
nonlinear stop, with the target exit commented out. I repeated the
procedure for the target exit with the volatility stop commented out. To
optimize the linear exits, I set a0 and a2 to zero and optimized a1 by
itself. All three constants (a0, a1, a2) were optimized together for the
nonlinear exits. In most cases, I optimized on net profit, unless doing
so was clearly inferior, such as generating an outsized drawdown. In
that case, I scanned the optimization results and chose the optimum
subjectively.
The results are shown
below in Fig. 2. To evaluate the results, I recorded the net profit,
profit factor, percentage of winning trades (out of total number of trades),
and the worst-case peak-to-valley drawdown for each optimization. The
best results for each comparison are highlighted in green in the figure.
For example, for T-bonds (US), the nonlinear stop had a higher net
profit, higher profit factor, greater percentage of winning trades, but
a larger worst-case drawdown compared to the linear stop. Overall, the
nonlinear exit tested better than the linear exit in 18 of 23 (78%)
comparisons.
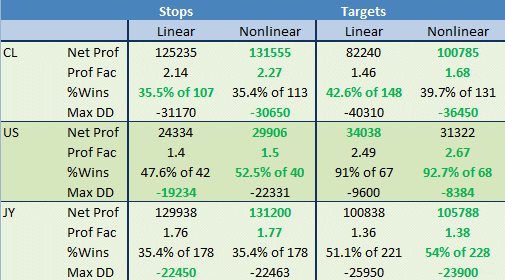
Fig. 2.
Volatility exit test results comparing linear and nonlinear exits for a
simple trend-following system. The superior performance metric is
highlighted in green for each comparison. Overall, the nonlinear exit
tested better in 18 of 23 comparisons.
Final
Thoughts
Based on the test results,
the nonlinear volatility exits seem to offer some advantage over the
standard linear exits. Of course, these are optimized results. However,
because I optimized both the linear and nonlinear exits separately, it
should be a fair comparison. Out-of-sample or real-time tracking results
are recommended before committing to this type of exit in practice.
One drawback of the
nonlinear exits is that they add two additional parameter values to your
system, which increases complexity and potentially decreases robustness.
Nonetheless, compared to a fixed size dollar stop, the normalized
nonlinear exit equation has several advantages, such as adapting
automatically to volatility and making it easier to optimize over
multiple markets. Once implemented, the parameters a0 and a2 could be
set to zero to revert to the linear exit if desired. Overall, these
exits may be worth considering for your next trading system project.