One money management technique that many traders use is a money management stop. A money management stop is a protective stop order placed below the entry price for a long trade or above the entry price for a short trade. It provides an automatic exit point in case the market reverses. Where the stop is placed often makes the difference between a good trade and a bad one. If the stop is placed too close to the entry price, the trade could be stopped out by normal market activity before the trade has a chance to develop. On the other hand, if the stop is placed too far from the entry, the loss could be much larger than necessary if the stop is hit.

Some common methods for selecting the placement of a money management stop include (1) fixed dollar amounts (e.g., a $200 stop in the E-mini S&P implies a stop size of four points), (2) support/resistance levels (e.g., recent highs/lows), and (3) a multiple of the average true range (ATR; e.g., three times the ATR below the entry for a long trade).

While all these methods have merit, they also have potential problems. Support and resistance levels tend to attract trading activity, so placing stop orders there can make it more likely the stop will be hit. Fixed dollar stops have the merit of simplicity but don't adapt to changes in market volatility. A $300 stop, for example, may be large enough when market volatility is low but may be too tight when the volatility increases. Taking a multiple of the average true range is a way to adapt to changing volatility, but the multiplier becomes another system parameter. There is typically no obvious way to choose the multiplier other than through back-testing, which effectively means optimization.

With this in mind, I decided to develop a money management stop that adapts to market volatility and requires no optimization. I call it a "noise tolerant" stop. It's based on the idea that market movement consists of two components: trend and noise. The trend component is what we're trying to trade; going long in an up trend or short in a down trend. Superimposed on the trend is the noise component. The noise component is all the up and down activity within the trend.

Notice that the definition of noise depends on the trend we're interested in. If, for example, we're trading one minute bars and our average winning trade lasts 15 minutes, then the trend is defined as what happens over that 15 minute period. In this case, the noise is the deviation from that 15 minute trend. On the other hand, if we're trading monthly bars where the average winning trade runs for, say, 14 months, then the noise is the deviation from that 14 month trend line. Clearly, the noise will be greater for a longer time frame.

As the name suggests, my noise tolerant stop is sized according to the noise component in the market. To determine the market noise, we detrend the price series and calculate the deviation of the prices for the detrended series. Consider the price series shown in Fig. 1, below.

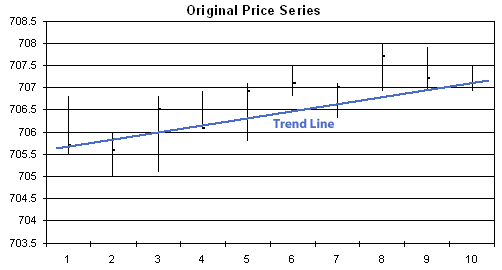
Figure 1. Original price series, prior to detrending.

A trend line has been drawn from the close of the first bar to the close of the last bar. This represents the trend component in the price series. To detrend the prices, we subtract this trend from the prices. The equation for the detrended prices is as follows:

    Detrended Price j = Price j - [ (C[N] - C)/N * j + C]

where Price j is the price j bars ago (e.g., j = 0 is the current bar; j = 1 is one bar ago, etc.), C[N] is the closing price N bars ago, C is the current close, and N is the number of bars back to the start of the trend. Price j can be any price on the bar, such as the high, low, open, or close.

Applying this equation to the price series in Fig. 1 results in the detrended price series shown below in Fig. 2. The prices are now centered around the zero axis. The noise can be defined as the deviation of price from this axis. The maximum deviation for this price series is noted in Fig. 2. For my noise tolerant stop, I first determine this maximum deviation then take the average of this value over the past N bars. I use the average maximum deviation from the detrended series as the size of the stop.

Figure 2. Detrended price series, obtained by subtracting the trend component from the prices shown in Fig. 1.

In EasyLanguage code for TradeStation, these calculations can be written as follows:

{
 Function NTStop
 Noise tolerant money management stop.

 This function detrends the price over the last N bars.
 The maximum deviation of price from the trend line is used
 to determine the size of the money management stop, which
 is returned.

 Copyright 2006 Breakout Futures
 www.BreakoutFutures.com

}
 input: N        (NumericSimple);    { Lookback length }
 
 Var:  HDet      (0),     { detrended high }
       LDet      (0),     { detrended low }
       Devi      (0),     { deviation from trend line }
       MaxDev    (0),     { maximum deviation }
       ii        (0);     { loop counter }
 
 { Calculate deviation of price from trend }

 MaxDev = 0;
 for ii = 0 to N Begin
     HDet = H[ii] - ((C[N] - C)/N * ii + C);
     LDet = L[ii] - ((C[N] - C)/N * ii + C);
     Devi = MaxList(AbsValue(HDet), AbsValue(LDet));
     if Devi > MaxDev then
        MaxDev = Devi;
 End;
  
 { Use average of MaxDev over past N bars as stop size }
 NTStop = Average(MaxDev, N);

This function can be downloaded from my web site on the free downloads page. It returns the size of the money management stop in points. A typical use of the function within a TradeStation strategy would be as follows:

  StopSz = NTStop(4);   { call the function to get the stop size }

  Sell next bar at EntryPrice - StopSz stop;  { stop price for a long trade }

  Buy to cover next bar at EntryPrice + StopSz stop;  { stop price for short trade }

where StopSz is declared as a variable.

You'll notice that this function has one parameter, the look back length, N. However, this value does not need to be optimized. N is number of bars in the trend. Since we are interested in sizing our stops so that our winning trades will not be stopped out by market noise, N can be chosen as the average length of the winning trades. In general, adding a stop to a system will change the length of the winning trade, so it may be necessary to first set N, run the system, check the length of the winning trades, and adjust N to match if necessary. Nonetheless, there is no optimization here. There is only one value of N that will correspond to the length of the average winning trade.

To illustrate this idea, I added this stop to Joe Krutsinger's Time Charger system (described below) to see how it compares to a fixed size stop for the same system. Here are the results (e-mini S&P MidCap 400 (EMD); $25 costs per contract; last four years):

Fixed size stop, as recommended by Joe:

    Net Profit: $27,475

    Profit Factor: 1.54

    % Wins: 52.9%

    639 trades

    Average Trade: $43.00

    Max Intraday Drawdown: -$2160.

Noise tolerant stop:

    Net Profit: $25,910

Overall, the results are similar. The fixed size stop appears to do a slightly better job overall, but, of course, the fixed size stop is optimized. The noise tolerant stop achieved these results with no optimization whatsoever. Notice that the percentage of winners is larger for the noise tolerant stop. This reflects the intended purpose of the stop, which is to avoid getting stopped out by normal market noise. To accomplish this, the noise tolerant stop will often be larger than a comparable fixed size stop, although they may be similar when the market volatility is low.

You might consider comparing this stop against your own fixed size or ATR-based stops. And remember that replacing an optimized stop with this one means one less system parameter to optimize.

Mike Bryant

Breakout Futures