The following article was originally published in the November 2008 issue of The Breakout Bulletin.
 

Do Changing Markets Invalidate Your System?

If you've traded the markets for any length of time, you've probably experienced the frustration that occurs when the market seems to start trading differently, and your previously successful system no longer seems to work. The recent increase in volatility in the stock indexes and the large intraday swings in these markets are a good example of changing markets. It's clear that the volatility has increased, but how can this be quantified and does it necessarily mean the system you're trading should no longer be trusted?

Statistical Approaches

A few straight-forward statistical tests can go a long way towards answering these questions. There are several possible approaches to this problem. One possibility is to test the market itself. Sherry and Sherry¹ presented a statistical test for nonstationarity of the markets based on the chi-square test. Nonstationarity is when the properties of a statistical distribution, such as the distribution of price changes in a financial market, change over time. A chi-square test can be used to determine if two cumulative distributions are significantly different. If the distribution of recent price changes is significantly different than the distribution of past price changes, the market is nonstationary, and methods that worked well in the past may no longer work as well.

The only drawback to testing the market for stationarity is that it doesn't directly test the object of greatest interest; namely, the trading system itself. An alternative approach is to test the technical indicators used in a trading system or method. For example, if a trading system uses moving averages and the average true range, we could look at how these indicator values have changed recently relative to their past values. To do this, we can compare the average value of the indicator calculated over all past data to the average calculated over recent data only. A statistical test can be used to tell us if the recent average is significantly different than the long-term average. If the two averages are far apart, they may not belong to the same statistical distribution. In that case, we might expect that the trading rules based on these indicators, which worked well in the past, may not work as well going forward.

Comparing Means

Comparing two means or averages is one of the most common tests in statistics. If we take a random sample from a larger population and calculate the mean of the sample, we can expect that it will be at least somewhat close to the mean of the population. If we repeatedly take random samples and calculate the mean of each sample, we could then plot a distribution of these means. The Central Limit Theorem of statistics tells us that this sampling distribution of means will be approximately normally distributed, regardless of the distribution of the population values, provided our sample size is large enough ("large enough" generally means a sample size of at least 30).² This is an important result for trading because most of the indicators we might use will not be normally distributed, which means they won't form that nice bell-shaped curve that's a necessary condition for many statistical tests.

For example, we could look at the values of an average true range indicator applied to daily bars over the past 10 years. It will almost certainly not be normally distributed. The Central Limit Theorem tells us that even if this distribution is highly skewed, bimodal, or some other strange shape, the sampling distribution of means calculated by randomly sampling from the original distribution will be nearly normal, provided our sample size is large enough. The Central Limit Theorem also states that if we take the average of all our sample means, that average will approach the population mean.

The standard deviation of the sampling distribution of means, called the standard error of the means, is equal to the standard deviation of the population divided by the square root of the sample size. In general, the standard deviation tells us how the values (in this case, the means) on the distribution are dispersed. For example, 95% of the means will be no more than 1.96 standard deviations from the population mean. This is referred to as the z score or critical ratio, which in this case can be written as follows:

z = (x - m)/(s/n^1/2)

where x is the sample mean, m is the population mean, s is the standard deviation of the population, and n is the sample size. The value 1.96 comes from the z or standard normal distribution tables. The area under the standard normal curve between the z values of -1.96 and +1.96 is 0.95 (95% of the total area).

There are several ways to use this equation. One way is as a test for stationarity of our indicators. If we calculate the z score repeatedly for samples of recent data and find that fewer than 95% of the z scores lie within -1.96 to +1.96, for example, then we can conclude that the recent data are part of a different distribution. In other words, the indicator is nonstationary. The statistical distribution of the indicator values has changed.

A second way to use the z score is to calculate it for the most recent sample. If the z score exceeds some threshold (say, greater than 1.96 or less than -1.96), then we may want to take some action based on the idea that the indicator is too far from the mean. In this case, we're not concluding that the recent sample is not part of the population necessarily, just that it's so far from the long-term mean that we're no longer confident that the system will work the same as it did before.

An S&P 500 Example

To illustrate these ideas, I looked at daily bars of the E-mini S&P 500 (symbol ES) over the ten year period ending Nov 5, 2008. I evaluated the following indicators on these data:

1. Close minus average close over the past 30 bars.

2. Average true range over the past 30 bars.

3. Slow D stochastic with a length of 14 bars.

4. ADX with a length of 14 bars.

5. The difference between the highest high and the lowest low over the past 30 bars divided by the average true range over the past 30 bars.

The first indicator measures trend direction as well as the magnitude of the trend. Indicator two is a measure of volatility. The slow stochastic is an overbought/oversold indicator with values ranging from 0 to 100. ADX measures the trend strength. The last one is a measure of the trend potential of the market normalized by volatility.

As an example of the type of distribution that these indicators produce, Fig. 1 plots the distribution of indicator 1 on the E-mini data. Notice that the distribution is skewed to the right, and there are a small number of very large negative values, reflecting large down days.

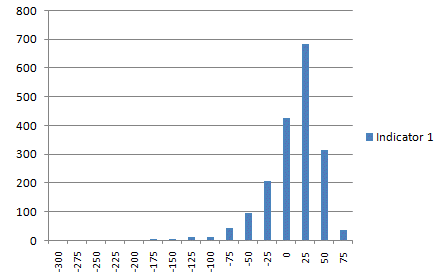
Fig. 1. Probability distribution of indicator #1 over 10 years of daily E-mini S&P 500 price data.

We can illustrate the Central Limit Theorem by plotting the sampling distribution of the means for this indicator, as shown in Fig. 2. Random samples were drawn from the population shown in Fig. 1, and the mean was calculated for each sample. Fig. 2 plots the distribution of these means. Notice that, as stated in the Central Limit Theorem, the distribution of the means is approximately normal, despite the fact that the original distribution is skewed.

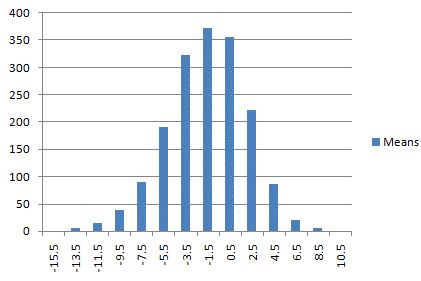
Fig. 2. Sampling distribution of the means for indicator #1.

To perform the z score calculations, I wrote a TradeStation strategy called TestMarketChange, which is available on my download page. TestMarketChange recorded the value of each indicator on each bar of data. The 10-year history of the ES consisted of a total of 2416 bars of data. Starting with bar number 2000, the strategy calculated the z score for the sample consisting of the most recent 100 bars of data. For each bar, it calculated the population mean and standard deviation over all data up through the current bar. The sample mean was calculated for the most recent 100 bars of data. The strategy then calculated the z score using the equation shown above, with n = 100.

TestMarketChange wrote out the z scores to the Print log in TradeStation. A partial listing is shown below.

End-of-Data Samples...
1,1070315,2.0995,-9.7463,4.8471,-1.0025,-2.2935
2,1070316,1.9137,-9.6604,4.6030,-0.8660,-2.4113
3,1070319,1.7821,-9.5689,4.3919,-0.7298,-2.5412
4,1070320,1.6655,-9.4762,4.2309,-0.6120,-2.6236
5,1070321,1.6033,-9.3704,4.1093,-0.5347,-2.6834
6,1070322,1.5360,-9.2636,4.0162,-0.4987,-2.7794
7,1070323,1.4712,-9.1602,3.9464,-0.5050,-2.9066
8,1070326,1.4310,-9.0610,3.9055,-0.5356,-3.0208
9,1070327,1.3878,-8.9619,3.8889,-0.5841,-3.1341
10,1070328,1.3227,-8.8602,3.8877,-0.6373,-3.2536
11,1070329,1.2992,-8.7608,3.9222,-0.6822,-3.3618
12,1070330,1.2877,-8.6507,3.9965,-0.7098,-3.4961
13,1070402,1.2969,-8.5394,4.1131,-0.7261,-3.6259
14,1070403,1.3074,-8.4253,4.2446,-0.7584,-3.6586
15,1070404,1.3125,-8.3108,4.3687,-0.8121,-3.6863
16,1070405,1.3279,-8.2005,4.4738,-0.8848,-3.7227
17,1070409,1.3739,-8.0941,4.5739,-0.9729,-3.7496
18,1070410,1.4263,-7.9912,4.6741,-1.0711,-3.8254
19,1070411,1.4501,-7.9113,4.7572,-1.1843,-3.8650
20,1070412,1.4670,-7.8374,4.8177,-1.3160,-3.8932
21,1070413,1.4889,-7.7685,4.8650,-1.4757,-3.8646
22,1070416,1.5365,-7.7014,4.9010,-1.6519,-3.7726
23,1070417,1.5900,-7.6404,4.9270,-1.8307,-3.6362
24,1070418,1.6434,-7.5866,4.9438,-2.0129,-3.4684
25,1070419,1.6915,-7.5318,4.9517,-2.2013,-3.3036
26,1070420,1.7654,-7.4761,4.9570,-2.3905,-3.0353
27,1070423,1.8390,-7.4204,4.9657,-2.5721,-2.7407
28,1070424,1.9636,-7.3717,5.0234,-2.7238,-2.4285
29,1070425,2.0983,-7.3315,5.1309,-2.8400,-2.0371

...

...

A total of 417 samples were taken. For example, sample 1 was calculated from bars 1901 to 2000, sample 2 from bars 1902 to 2001, until the 417th sample was calculated from bars 2317 to 2416. Each line shown above lists the sample number, date in TradeStation format, and the z scores for the five indicators (left-to-right order).

A second part of the TestMarketChange strategy counted the number of occurrences of each sample for which the absolute value of the z score was less than or equal to 1.96. As explained above, 95% of random samples drawn from the population will have z scores between -1.96 and 1.96. These results, which were also written to the print log, are shown below.

Clearly, none of the percentages approaches the 95% value we would expect for random samples drawn from the population. This suggests that these samples of recent data are fundamentally different from the overall population. In other words, recent values of the indicators are distributed differently than past data, which means the distribution is nonstationary. It changes over time.

What to Do When Indicator Means Change

This analysis raises two main questions. First, if you find that the distributions of the indicators used in your trading system are nonstationary, what should you do? Second, regardless of whether the distribution is stationary or not, if the mean over current data is significantly different than the population mean, what can be done?

One way to address nonstationarity is to search for indicators that are relatively stable. For example, note that the mean of indicator #4, the ADX, remained relatively close to the population mean on recent samples 54% of the time. Perhaps other indicators could be found with even higher percentages. Basing a trading system on such indicators might generate better walk-forward results than using indicators with low percentages.

An example of an indicator with a low percentage is indicator #2, the average true range (ATR). As shown above, the ATR was far from the population average on 95% of recent samples. This is no doubt due to the abnormally high volatility in recent months. This suggests that using the ATR directly in a trading rule (e.g., "if ATR >= 15, then ...") could lead to poor results. However, if the ATR is used to normalize another indicator or value, such as in indicator #5, this problem might be mitigated.

As to the second question, there are several possible solutions when the mean over current data is significantly different than the population mean:

1. Skip upcoming trades; i.e., only take trades when the indicators are part of the population, as determined by the z score.

2. Re-optimize the system over recent data.

3. Develop different trading rules for different ranges of the indicators. When the indicator mean moves to a different range, the rules for that range would take effect.

Final Thoughts

This article only scratches the surface of the topic of nonstationary distributions in trading. I chose to analyze the distributions of indicators rather than the market itself because most trading systems use one or more indicators. When the indicators change significantly, it implies that the system based on them may no longer be valid.

Nonstationary indicators and/or markets tend to support the idea of periodic re-optimization of trading systems. If the market has changed in some fundamental way, it may be necessary to re-optimize. However, this alone won't guarantee success. If the changes happen too fast, it may be difficult to keep up. That's why I suggested finding indicators that have relatively stable distributions. While this won't guarantee the future, either, it may provide enough stability for profits until the next change is necessary.

Notes:

1. Sherry, Clifford J. and Sherry, Jason W. The Mathematics of Technical Analysis. iUniverse.com Inc, Lincoln, NE, 2000.

2. Strictly speaking, the shape of the sampling distribution of means approaches the normal distribution as the number of samples approaches infinity.

Copyright © 2001-2013 Breakout Futures

Copyright © 2013-2017 Adaptrade Software