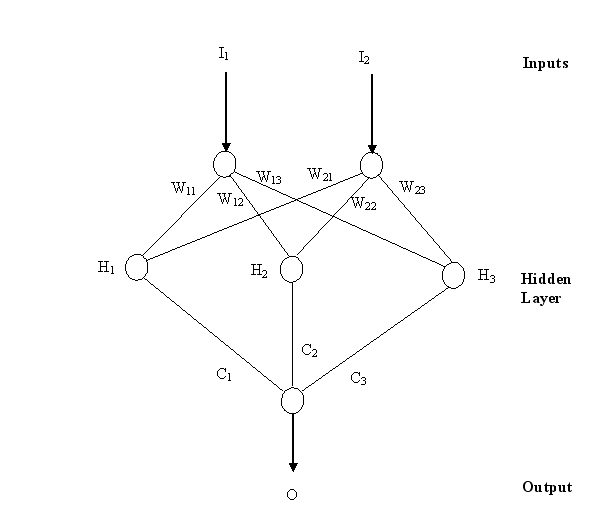
Figure 1. A simple neural network with two inputs and a
single output.
The output, O, is produced from
the following equations (also see ref. 2):
H1 =
tanh(w11 * I1 + w21 * I2)
H2 =
tanh(w12 * I1 + w22 * I2)
H3 =
tanh(w13 * I1 + w23 * I2)
O = tanh(c1
* H1 + c2 * H2 + c3 * H3)
I1 and I2 are the two inputs.
These could be anything that might have some predictive value for trading, such
as momentum, stochastics, ADX, moving averages, etc. A complex network might
have dozens of inputs. The weights are w12, w12, w13,
w21, w22, w23, c1, c2, and c3. These will be determined by fitting the
model ("training the network") to the data. The hyperbolic tangent function,
tanh, returns a value in the range [-1, 1], so the output, O, will lie in
this range. The inputs I1 and I2 are typically scaled so that they also lie
in the range [-1, 1].
The process of establishing the
neural network is called training. It involves iterating on the weights
using known input-output data. For example, the output O might be interpreted as
a bullish/bearish signal, with values near +1 bullish and values near -1
bearish. Bullish and bearish patterns on a price chart would be identified and
the corresponding inputs I1 and I2 recorded. This would give us sets of training
data: (I1-1, I2-1, O-1), (I1-2, I2-2, O-2), (I1-3, I2-3, O-3), etc. The model,
as given by the equations, would be applied to these examples, and the weights
adjusted until the network correctly identified the bullish and bearish
patterns. The technique traditionally used to adjust the weights in an iterative
manner is called back-propagation.
Once the network is trained, it
can be tested out-of-sample to make sure it is not over-fit to the training
data. Out-of-sample testing simply means the network is tested on data that was
not used during the training. If it performs well on the out-of-sample data, it
can be deemed a successful model.
As you might guess, we are not
going to try to replicate all these steps precisely in our EasyLanguage trading
system. For one thing, TradeStation doesn't provide a back-propagation
algorithm, so we will have to rely on its built-in optimization feature by
making the weights for the network inputs to our system. That way, we can
optimize on the weights using the system parameter optimization feature of
TradeStation. Secondly, there's no easy way in TradeStation to provide training
data sets to the model. Instead, we'll train the network directly on the price
data by incorporating the network into a trading system and optimizing the
weights of the network as part of the trading system. This approach is not ideal
from an optimization standpoint, but is more direct and is consistent with the
limitations of TradeStation.
For our trading system, we'll
take the inputs to the neural network as follows:
I1 = (C -
C[2])/33
I2 = (C -
C[10])/64
These are the two and 10-day
momentum, normalized to keep them in the range [-1, 1]. The output will be
interpreted as a bullish/bearish signal, such that
O >= 0.5
--> bullish
O <= -0.5
--> bearish
On a bullish signal, we'll
place an order to buy at the prior day's high on a stop. On a bearish signal,
we'll place an order to sell at the prior day's low on a stop. For simplicity,
all trades will be exited after two days, and no protective stop will be
used. The complete system code is shown below in Fig. 2.
{
NN Inspired
This system uses a neural
network-like function to trigger entry. The "weights" of
the network
are determined by optimization within TradeStation.
Mike Bryant
Breakout Futures
www.BreakoutFutures.com
mrb@BreakoutFutures.com
Copyright 2003 Breakout Futures
}
Inputs: w11
(0), { weights
}
w12
(0),
w13
(0),
w21
(0),
w22
(0),
w23
(0),
c1
(0),
c2
(0),
c3 (0);
Var: I1
(0), { input 1
}
I2 (0), { input 2
}
H1 (0), { hidden node 1
}
H2 (0), { hidden node 2
}
H3 (0), { hidden node 3
}
NNOut
(0); { function output }
{ Define inputs: 2 and 10-day momentum, scaled
}
I1 = (C - C[2])/33;
I2 = (C -
C[10])/64;
{ Define "neural net" function }
H1 =
tanh(w11*I1 + w21*I2, 50);
H2 = tanh(w12*I1 + w22*I2, 50);
H3
= tanh(w13*I1 + w23*I2, 50);
NNOut = tanh(c1*H1 + c2*H2 + c3*H3,
50);
{Print("date: ",
date:8:0, " NN Output: ", NNOut:6:3);}
{ Place trades based on function output }
If
NNOut >= 0.5 then
Buy next bar at High
stop;
If NNOut <= -0.5 then
Sell
short next bar at low stop;
If BarsSinceEntry = 2 then Begin
Sell this bar on close;
Buy to cover this bar on
close;
End;
Fig. 2. EasyLanguage
code for neural network-inspired system, "NN
Inspired".
Our "training" period will be
on daily data for the E-mini S&P, from 9/1997 to 12/31/1999. $75 will be
deducted from each trade for slippage and commissions. We'll optimize the nine
network weights over this data, then test the system out-of-sample for one year,
from 1/1/2000 to 12/31/2000. Because of the large number of inputs, we'll limit
the parameter values to -1, 0, +1. Every combination of weights with the values
-1, 0, +1 will be tested by the optimization process. This gives us 3 to the 9th
power or 19683 optimization trials. On my 2.2 GHz computer, this took
approximately 1.5 hours in TradeStation 7.1.
The resulting optimal weights
were:
w11 =
-1
w12 =
0
w13 =
1
w21 =
-1
w22 =
1
w23 =
-1
c1 =
1
c2 =
-1
c3 =
1
Here are the optimized
results:
Net Profit:
$17,700
Profit Factor:
1.47
No. Trades:
99
% Profitable:
52%
Ave. Trade:
$179
Max DD:
-$6,813
I then tested the system
out-of-sample over the year following the optimization period. Over this period
(1/1/00 to 12/31/00), the system produced the following
results:
Net Profit:
$12,863
Profit Factor:
1.56
No. Trades:
51
% Profitable:
55%
Ave. Trade:
$252
Max DD:
-$10,325
The fact that the system traded
profitably on data not used in the optimization is a good sign. However, using
other optimization periods, the walk-forward (out-of-sample) results did not
always hold up. In particular, the last two years or so seem to be fundamentally
different than the prior five or six years. While it's possible to optimize
successfully up through, say, June 2003, the best results are achieved with
relatively fewer trades than in prior years. That doesn't leave enough data from
June forward to test the system out-of-sample.
Finding a good balance between
the optimization and evaluation periods is always a challenge. There needs to be
enough data in the optimization period to avoid over-fitting the system, but you
have to leave enough data to properly evaluate the system. If the optimization
period ends too far back, the market dynamics in the evaluation period may be
markedly different from the optimization period, rendering the optimized results
useless going forward. One way to address this problem
is to shorten the time scale. Instead of developing a system for daily bars,
focus on intraday data. That makes it possible to have more data over a shorter
time period, where the market dynamics may be more stable. It would be
interesting here to apply our system to hourly bars. The system could be
modified slightly to buy/sell in the morning and exit on the close. The
resulting increase in the number of trades may make it possible to include both
optimization and evaluation periods within a shorter time frame, so that the
optimized results would be more valid going
forward.
Despite the
inherent complexity of neural networks, hopefully I've demonstrated that
some of the basic features of neural networks can be incorporated into even a
simple trading system. By using the tanh function and the basic structure of a
neural network, we've essentially added a nonlinear indicator to a simple
trading system. One of the primary limitations was that the number of inputs
(i.e., the network weights) was so large that we had to restrict our
optimization to the values -1, 0, 1. However, this process could be viewed
as a screening step for the weights. There's nothing preventing us from refining
the optimization during a second pass. For example, if the optimal weight from
the first pass was +1, we could go back and try values between 0.5 and 1.5.
Similarly, for optimal values of -1, we could try values between -0.5 and -1.5
on a second pass. We might also try reducing the number of nodes in the hidden
layer. This would reduce the number of weights. Different or additional inputs
could also be tried.
The primary
benefit of a neural network approach is the nonlinear structure of the
functions composing the network. Nonlinear functions are better suited to the
complexity of market data than linear functions. The biggest problem is probably
the tendency to over-fit the network to the training data. If you decide to
pursue this approach further, don't forget to thoroughly test any system
out-of-sample, if not in real-time tracking, before committing real
money.
That's all for now. Good luck with your
trading.
References:
-
Joe Krutsinger,
The Trading Systems Toolkit, Probus Publishing Co., Chicago, 1994.
-
Guido J. Deboeck, Trading on the
Edge, John Wiley & Sons, Inc., New York, 1994.