The Breakout
Bulletin
The following article was originally published in the December 2011 issue of
The Breakout Bulletin.
What's Wrong with ATR Stops?
Most traders probably consider
protective stops an essential element of their trading strategies.
Deciding where to place the stops is another matter. One of the most
recommended methods for placing stops uses the average true range (ATR).
The ATR is often used as a proxy for market volatility, and ATR stops
are intended to adapt the size of the stop to market volatility.
The calculation for an ATR stop is as
follows:
LStop = EntryPrice - MMFrL *
AvgTrueRange(NATRMML);
This provides the stop price for a long trade given the trade entry
price (EntryPrice), a multiplying factor (MMFrL), and the averaging
length (NATRMML) for the average true range function (AvgTrueRange). The
equation subtracts a multiple of the ATR from the entry price to obtain
the protective stop price. For a short trade, you would want the stop
price to be above the entry, so you would add a multiple of the
ATR to the entry price.
The logic behind the ATR stop seems sound enough. As shown below in Fig.
1, the trend on a price chart can be represented by a line that fits
approximately through the center of the price bars. The height of the
price bars -- their low-to-high range -- represents fluctuations in
price relative to the trend line. These fluctuations appear to be random
"noise" relative to the trend line. The bar's range (or true range*)
would therefore appear to be a good proxy for the noise in the market.
* true range is essentially the range adjusted for gaps.
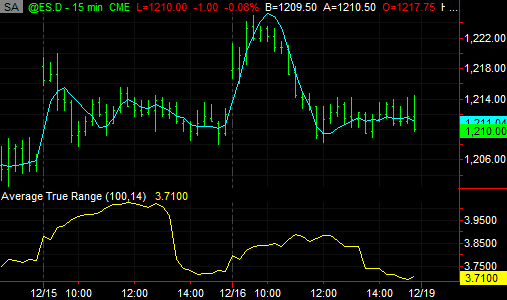
Figure 1. Typical price chart
illustrating average true range as a proxy for random market
fluctuations.
The argument for the ATR stop is that you want to place your protective
stop so that you avoid being stopped out on the random fluctuations but
you get out on larger moves. Some multiple of the ATR relative to the
entry would presumably accomplish that goal assuming the ATR is a good
representation of the noise in the market.
A Comparison with Other Stops
Despite the logic behind the ATR stop, a number of traders I've spoken
to avoid the ATR stop in favor of simpler stops. They cite either no
benefit or, worse yet, find that it doesn't hold up well in
out-of-sample testing or real time trading. My own experience is
similar. If the ATR stop makes so much sense, the performance advantage
should be apparent in back-testing compared to other types of protective
stops. Secondly, the parameters of the stop (multiplying factor and
look-back length) should hold up in out-of-sample testing and real-time
tracking and trading. This rarely seems to be the case, however.
To see why the ATR stop often fails to live up to its promise, it's
helpful to compare it to other, common stop types. In particular,
consider the fixed dollar stop and the percentage stop.
The fixed dollar stop places the protective stop so that if it's hit,
the loss will be a specified dollar amount, such as $500. For example, a
$500 dollar stop for the E-mini S&P futures corresponds to 10 points (10
points x $50 per point for the E-mini = $500), so the stop would be
placed 10 points below the entry for a long trade.
The percentage stop is commonly used for stock trading. It allows you to
specify the maximum percentage loss you want in the trade. With a 2%
stop, for example, if the stop is hit, the loss will be 2% of the trade
value. To calculate the stop price for a percentage stop, multiply the
percentage by the entry price and subtract (for a long trade) the result
from the entry price. For example, for a 5% stop, if the entry price is
30, the stop price for a long trade would be 30 - (0.05 x 30) or 28.50.
If the stop is hit, the loss would be 30 - 28.5 or 1.5 points per share,
which is 5% of the trade.
To compare the three types of stops, I calculated the parameter values
for each stop type over the range of stop values from $100 to $1000.
These are the stop sizes in dollars; that is, the amount lost if the
stop is hit. To find the ATR and percentage stop parameter values over
this range, it's necessary to know how the ATR and prices, respectively,
vary over the price history of interest.
As an example, I took the last six months of 15 minute bars of the
E-mini S&P 500 day session futures. The table below shows the min and
max values of the E-mini futures price and the 100-bar ATR over the time
period.
This means that if the ATR multiplier is between 0.911 and 1.716, the
ATR stop will be between $100 and $1000 for any bar on the chart.
Likewise, a stop percentage between 0.188% and 1.49% will give a stop
between $100 and $1000 for any bar on the chart.
Now that the three types of stops are normalized to the same range of
values, consider how the stop sizes vary over the bars in the chart for
a given stop parameter value. Using the midpoint values for the ATR and
percentage stops from the table above gives, respectively, an ATR
multiple of 1.31 and a percentage stop value of 0.84%. To see how the
respective stop sizes vary, these values can be applied to the min and
max ATR and price values from the first table. The result is shown below
in Fig. 2.
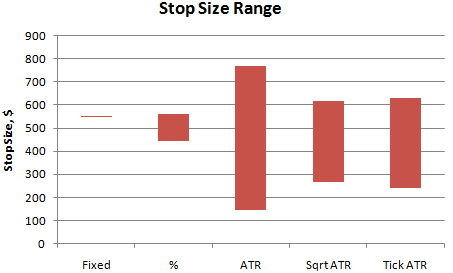
Figure 2. Range of stop sizes
for different types of protective stops over six months of E-mini S&P
prices.
The midpoint of the fixed dollar stop is shown as the thin horizontal
line on the left ("Fixed"). This is simply the fixed dollar stop of $550
(half-way between $100 and $1000). The percentage stop calculated using
the midpoint percentage value is shown as the "%" bar. Because the
percentage stop is calculated from price, it varies over the six-month
price history of the E-mini as the price itself varies. This gives a
range of stops from about $450 to $560.
Now consider the ATR stop. The long vertical bar ("ATR") in the chart
represents the range of stop sizes calculated using the midpoint ATR
multiplier. Because the ATR varies from roughly 2 to 12 over the price
history, the size of the ATR stop varies from about $150 to $770. In
terms of E-mini points, this means that the size of the protective stop
could be anywhere from 3 points to 15 points, depending on when the stop
is placed.
Keep in mind that this range of stop values for the ATR stop is for a
given parameter value calculated over only six months of history. If the
same parameter value were used over a longer history, the range of stop
values would be even greater. In my opinion, it's this wide range of
stop sizes that's the Achilles heel of the ATR stop. Only if you believe
that the market volatility changes so much over six months that you
would want a stop size of 3 points one day and 15 points a few days
later does the ATR stop make sense.
Why Does the ATR Vary so Much?
Although the ATR appears to be a reasonable way to quantify volatility,
it varies much more than one would expect. The reason for this may have
to do with how the ATR is plotted. The calculations above were performed
on a chart of 15 min bars. Anyone who follows the markets on an intraday
basis knows that during certain periods, the markets can be very quiet,
with relatively little volume. These periods are often followed by
periods of intense action, with high volume and volatility.
During periods of low volume, it's likely that the bars on a time-based
price chart will have a low range. Bars that overlap periods of high
volume will likely have a higher range. Roughly speaking, the price
change per unit of trading volume may be approximately constant, whereas
the price change per unit of time is likely to vary quite a bit. This
may account for the high variation in the ATR on time-based price
charts.
To confirm this hypothesis, the same analysis performed above was
repeated for a 20,000 tick chart of the same six months of E-mini price
history. Tick bars were chosen because each tick bar represents the same
number of transactions and therefore approximately the same volume
(volume bars could also be plotted in TradeStation with similar
results). The tick size was set to 20,000 because that value gave nearly
the same number of bars as on the 15 min bar chart.
The results are shown above in Fig. 2. The bar on the right-hand side
("Tick ATR") shows the range of stop sizes for an ATR stop calculated
from the 100-bar ATR obtained from the tick chart using the midpoint
fraction for stop sizes between $100 and $1000. As can be seen, the
range is much lower when tick bars are used, with stops ranging from
$240 to $630. This supports the idea that the variation in ATR on price
bars is related to the variation in volume from bar to bar on those
charts.
Conclusions
If you've found that ATR stops don't
work as well as you expected, it may be because the ATR calculated on
time-based bars, such as 15 min bars, varies more than you realize,
resulting in stops that vary in size too much to be practical for your
strategy. One way to address this may be to use tick bars that are
roughly equivalent in number to the time-based bars you were using. As
shown above, this can reduce the range of the ATR over the price
history. Other alternatives include using a fixed dollar stop or a
percentage stop. However, neither of these may vary enough with the
market's volatility to avoid stopping you out on the market's random
fluctuations.
Another option is illustrated above in
Fig. 2 above the label "Sqrt ATR". This bar shows the range of stop
values for a protective stop calculated the same way as the ATR stop on
15 min bars but using the square root of ATR, rather than the ATR
itself. The square root function tends to attenuate the high and low
values, compressing the range. This can compensate to some extent for
the wide variation in ATR values on time-based bars, leading to a stop
that still varies with market noise but not as widely as the basic ATR
stop. The range compression will be greater for larger ranges of ATR.
I'm not suggesting that ATR stops should be avoided on time-based bars.
Rather, the goal of this study was to understand why they often seem to
perform worse than expected given their apparent attributes. If you
conclude the ATR stop in your strategy is not performing as you think it
should, perhaps this analysis can help explain the problem. And
hopefully one of the suggestions offered above can help as well.
Mike Bryant
Breakout Futures
HYPOTHETICAL OR
SIMULATED PERFORMANCE RESULTS HAVE CERTAIN INHERENT LIMITATIONS. UNLIKE
AN ACTUAL PERFORMANCE RECORD, SIMULATED RESULTS DO NOT REPRESENT ACTUAL
TRADING. ALSO, SINCE THE TRADES HAVE NOT ACTUALLY BEEN EXECUTED, THE
RESULTS MAY HAVE UNDER- OR OVER-COMPENSATED FOR THE IMPACT, IF ANY, OF
CERTAIN MARKET FACTORS, SUCH AS LACK OF LIQUIDITY. SIMULATED TRADING
PROGRAMS IN GENERAL ARE ALSO SUBJECT TO THE FACT THAT THEY ARE DESIGNED
WITH THE BENEFIT OF HINDSIGHT. NO REPRESENTATION IS BEING MADE THAT ANY
ACCOUNT WILL OR IS LIKELY TO ACHIEVE PROFITS OR LOSSES SIMILAR TO THOSE
SHOWN.