Consolidation patterns can also
form other shapes, such as flags and triangles. Usually, a consolidation pattern
occurs after a large move. In his book, "7 Chart Patterns That Consistently Make
Money," Ed Downs (see reference) cites consolidation patterns as the best tool
to predict market direction. There are typically two methods for trading
these patterns. You can enter on a breakout from the pattern by buying when
the market moves above the upper boundary or selling on a downside breakout
below the lower boundary. The second method is to trade within the pattern by
selling at the upper boundary and buying at the lower boundary.
For the purposes of this
article, I'm going to restrict the definition of consolidation patterns to
horizontal trading range patterns, such as those shown in Figs. 1 and 2. To
quantify the definition, I'm going to say that a consolidation pattern is a
sequence of bars on the chart where the "density" of the bars is greater than
some threshold. To understand what I mean by "density," imagine drawing a
rectangle around the price bars in the consolidation pattern, as I've done in
Figs. 1 and 2. The rectangle surrounds the highest high and the lowest low of
the bars in the pattern. The more completely the bars fill up the rectangle, the
higher the density.
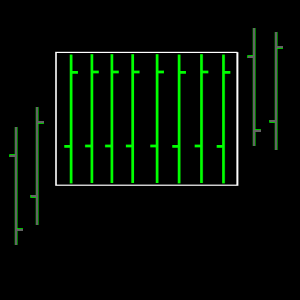
Figure 3. A rectangle bounds a consolidation pattern with the
highest possible density.
The highest possible density
for a rectangular consolidation pattern is shown in Fig. 3. In
this case, every bar spans the full height of the bounding
rectangle. In physics, density is defined as mass per unit volume; the more
mass contained within a given space, the higher the density. In our definition,
the more bar area within the bounding rectangle, the higher the density. The
"bar area" of the pattern can be defined as the sum of the heights of the
bars within the bounding rectangle. By bar height, I mean the high minus the low
or, to take gaps into account, the true range.
The area of the bounding
rectangle is the number of bars in the pattern multiplied by the highest high
minus the lowest low of the bars in the pattern; i.e.,
Area
(bounding rectangle) = N * (Highest High - Lowest Low)
where N is the number of bars
in the pattern. By this definition, the area of the bounding rectangle is the
same as the bar area for the densest pattern, shown in Fig. 3.
The density of any pattern
of price bars can now be defined as the bar area divided by the area
of the bounding rectangle; i.e.,
Density =
Sum of true ranges / [N * (Highest High - Lowest Low)].
By this definition, the pattern
shown in Fig. 3 will have a density of 1. This is the highest possible
density. Any other pattern will have a density value less than 1. The more
completely the bars fill up the bounding rectangle, the closer the density will
be to 1. Also note that since we've normalized the bar area by
the area of the bounding rectangle, the density value is independent of the
number of bars, so we can compare consolidation patterns with different
numbers of bars.
Now that we can calculate
the density of a consolidation pattern, how do we identify those patterns? The
key concept is that we're going to restrict our search for consolidation
patterns to the current bar. We want to know if the current bar is part of a
consolidation pattern. We could, in principle, extend the search to past price
patterns, but since we can't trade in the past, the more important task is to
determine the status of the current bar.
The approach is as follows: We
start by looking at a minimum number of bars, NBMin. We calculate the density of
the past NBMin bars. We then add one more bar to the search, and calculate the
density of the past NBMin + 1 bars. We keep adding bars to the search,
calculating the density of the pattern, until we reach some maximum number of
bars, NBMax. For example, we might consider all patterns from four to 20
bars in length. Each pattern begins at the current bar and looks backwards. We
want to find the pattern with the greatest density since this is most likely to
be a consolidation pattern. Once we find this pattern, we record its density and
the number of bars in the pattern. For example, we might find that the
last six bars have the highest density.
The pattern with the highest
density is our candidate consolidation pattern. To decide whether the
candidate is an actual consolidation pattern, we have to establish a threshold
value for the density. For example, we might decide that any pattern with a
density greater than 0.6 is a consolidation pattern. I'll suggest how to come up
with the threshold value shortly.
I programmed
this method in EasyLanguage using two functions and one indicator. The function
CPDensity calculates the density of the consolidation pattern. The function
CPLocate calls CPDensity and determines whether the current bar is part of a
consolidation pattern. CPLocate returns "true" if the current bar is part of a
consolidation pattern and "false" otherwise. CPLocate also returns the density
of the pattern, the number of bars in the pattern, and the upper and lower
bounds of the pattern through its argument list. Finally, the indicator
CPIndicate calls the CPLocate function and plots the upper and lower bounds of
the consolidation pattern on the screen if the current bar is part of a
consolidation pattern. CPIndicate also writes the results returned by CPLocate
to the TradeStation MessageLog.
{
Function: CPDensity ("Consolidation Pattern
Density")
Calculates the "density" of a consolidation/trading range
pattern
over the past NBars bars. The density is defined as the area of
bars in
the pattern divided by the maximum possible area. Area is
defined as
the sum of the height of the bars, where height is given by
the
true range. The max possible area is the area of the
rectangle
that bounds the bars; i.e., the highest high minus the lowest
low
times the number of bars.
Michael R. Bryant
Breakout
Futures
www.BreakoutFutures.com
Copyright 2003 Breakout Futures
August 2003
}
Input:
NBars (NumericSimple); { number of
bars in pattern }
Var: CPWidth
(0), { highest high minus lowest low over last NBars
bars }
NB (0),
{ equal to NBars, provided NBars > 0
}
SumTR (0), { sum of true
ranges over NB bars }
ii (0);
{ loop counter }
{
Make sure the input value of NBars is greater than zero }
NB =
MaxList(NBars, 1);
{
Calculate width of rectangle bounding consolidatin pattern }
CPWidth =
Highest(H, NB) - Lowest(L, NB);
{
Calculate sum of true ranges }
SumTR = 0;
For ii = 0 to NB - 1
Begin
SumTR = SumTR +
TrueRange[ii];
End;
{
Return sum of true ranges in pattern divided by max area of pattern
}
CPDensity = SumTR/(CPWidth * NB);
{
Function: CPLocate
Determine if current
bar is part of a consolidation/trading range
pattern. Return true if it
is; false otherwise.
The pattern is identified as follows:
1.
Patterns of length NBMin to NBMax are scanned using the
function CPDensity, which calculates the "density" of
the
consolidation pattern. All patterns start at the
current
bar.
2. The length of the pattern with the highest density
is
recorded.
3. If the density of the highest
density pattern matches or
exceeds a threshold level, the
pattern is considered to be
a consolidation pattern, and
TRUE is returned.
The function also returns the density, length (in
bars),
and the upper and lower boundaries of the pattern with the
highest
density.
Michael R. Bryant
Breakout
Futures
www.BreakoutFutures.com
Copyright 2003 Breakout Futures
August 2003
}
Input: DensTH
(NumericSimple), { Density threshold
}
NBMin (NumericSimple), { Min # of bars
in pattern }
NBMax (NumericSimple), { Max # of bars
in pattern }
PatDens (NumericRef), { Density
of pattern }
NBars (NumericRef),
{ Number of bars in pattern }
HBound (NumericRef), {
Upper/high boundary of pattern }
LBound (NumericRef); {
Lower boundary of pattern }
Var: MaxDens
(0),
{ max density found }
NMaxDens
(0),
{ length of pattern of max density
}
ibars
(0);
{ loop counter }
{
Search for pattern with highest density }
MaxDens = 0.;
For
ibars = NBMin to NBMax Begin
PatDens =
CPDensity(ibars);
If PatDens > MaxDens then
Begin
MaxDens =
PatDens;
NMaxDens =
ibars;
End;
End;
{
Record results for densest pattern for return }
PatDens =
MaxDens;
NBars = NMaxDens;
HBound = Highest(H,
NBars);
LBound = Lowest(L, NBars);
{
Check if densest pattern exceeds threshold }
If MaxDens >= DensTH
then
CPLocate = True
Else
CPLocate = False;
{
Indicator: CPIndicate
Plot the upper and
lower bands of consolidation patterns identified
by function CPLocate.
Michael R. Bryant
Breakout
Futures
www.BreakoutFutures.com
Copyright 2003 Breakout Futures
August 2003
}
Input: DensTH
(0.55); { Density threshold }
Var: NBMin
(4), { Min # of bars in pattern
}
NBMax (30), { Max # of
bars in pattern }
PatDens (0), { Density of
pattern }
NBars (5), { Number
of bars in pattern }
HBound (0), { Upper/high
boundary of pattern }
LBound (0), { Lower
boundary of pattern }
LocTF (false); { output of CPLocate function
}
LocTF = CPLocate(DensTH, NBMin, NBMax, PatDens, NBars,
HBound, LBound);
MessageLog(" Date: ", Date:6:0, " Time: ", time:6:0, "
Density: ", PatDens:6:3, " # Bars: ", NBars:3:0);
If
LocTF then Begin
Plot1(HBound,
"Upper");
Plot2(LBound, "Lower");
End;
So how well does
this method work? Take a second look at Figs. 1 and 2, above. Notice where I
identified the consolidation patterns on the charts. Below, in Figs. 4 and 5,
are the same charts, showing where the CPIndicate indicator has found
consolidation patterns. CPIndicate places red and blue crosses at the upper and
lower boundaries of the consolidation pattern it finds -- if any -- on the
current bar. I used a density threshold value of 0.6 in this case, with NBMin =
4 and NBMax = 30.
For the most
part, the consolidation patterns identified by CPIndicate are the same as those
I identified by eye.